The Mathematics of Sic Bo

• Sic Bo Results 2020
• Sic Bo Results Ufc
• Sic Bo Results Football
• Sic Bo Results 2019
• Super Sic Bo Results

By

Sic Bo was so popular in ancient times that it was one of the Big Four Chinese games. It was categorized as a Fortune game. Ancient people used to test themselves rather than winning money, which is the prime motive these days. The Mathematics of Sic Bo. Michael Shackleford. January 21, 2005. Sic Bo, meaning 'dice pair' is an ancient Chinese gambling game. Today it is one of the lesser known casino games and is often confined to designated rooms for Asian games. The game uses three dice and a table with a variety of betting options on the roll of those dice.

Michael Shackleford

January 21, 2005

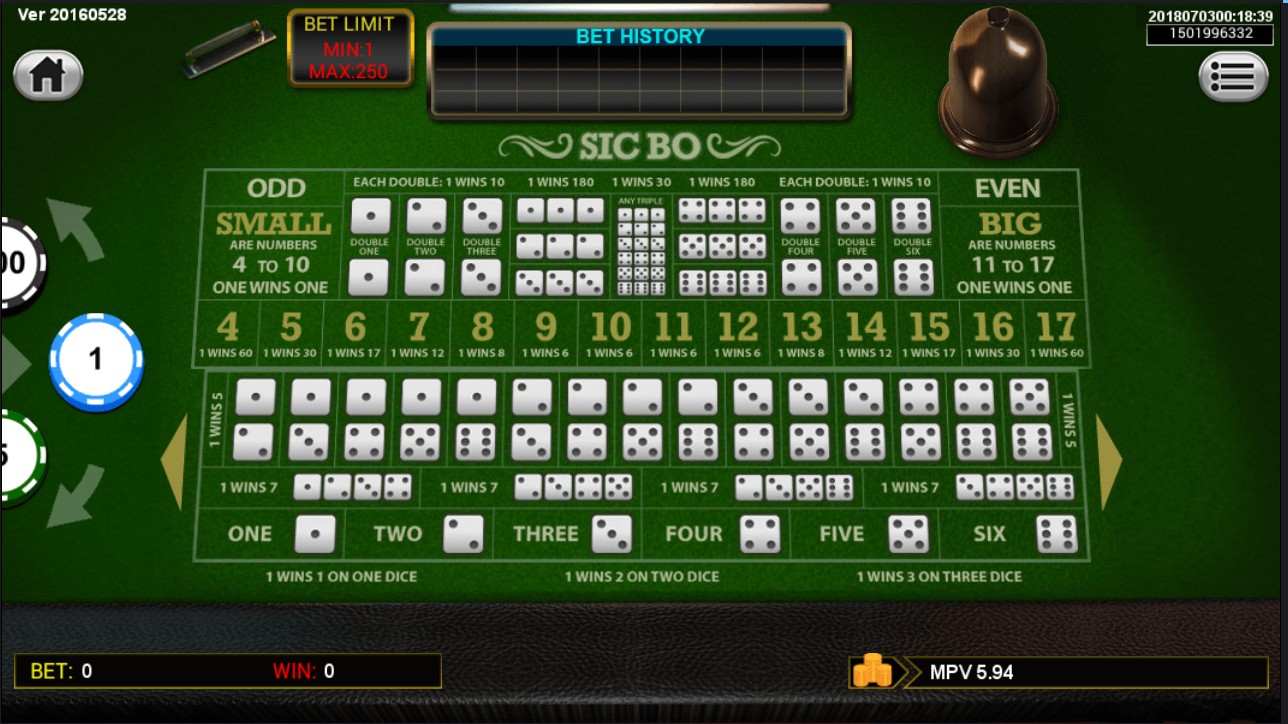
Sic Bo, meaning 'dice pair' is an ancient Chinese gambling game. Today it is one of the lesser known casino games and is often confined to designated rooms for Asian games. The game uses three dice and a table with a variety of betting options on the roll of those dice. The odds and table layout may also vary from place to place. If you must play Sic Bo I would suggest sticking to only the 'low' and 'high' bets.

Following is a list of the bets available. The payoffs listed are for Atlantic City and the Mirage in Las Vegas. Other casino’s odds will vary.

• Small: Wins on total of 4-10, except for a three of a kind. Pays 1 to 1.
• Big: Wins on total of 11-17, except for a three of a kind. Pays 1 to 1.
• 4: Wins on total of 4. Pays 60 to 1.
• 5: Wins on total of 5. Pays 30 to 1.
• 6: Wins on total of 6. Pays 17 to 1.
• 7: Wins on total of 7. Pays 12 to 1.
• 8: Wins on total of 8. Pays 8 to 1.
• 9: Wins on total of 9. Pays 6 to 1.
• 10: Wins on total of 10. Pays 6 to 1.
• 11: Wins on total of 11. Pays 6 to 1.
• 12: Wins on total of 12. Pays 6 to 1.
• 13: Wins on total of 13. Pays 8 to 1.
• 14: Wins on total of 14. Pays 12 to 1.
• 15: Wins on total of 15. Pays 17 to 1.
• 16: Wins on total of 16. Pays 30 to 1.
• 17: Wins on total of 17. Pays 60 to 1.

• Two of a kind: Player may bet on any of the 15 possible two dice combinations (for example a 1 and 2). Bet wins if both numbers appear. Probability of winning is 13.89%. Pays 5 to 1.
• Double: Player may bet on any specific number (for example a 1). Player wins if at least 2 of the 3 dice land on that number. Probability of winning is 7.41%. Pays 10 to 1.
• Triple: Player may bet on any specific number (for example a 1). Player wins if all 3 dice land on that number. Probability of winning is 0.46%. Pays 180 to 1.
• Any Triple: Wins on any three of a kind. Pays 30 to 1.
• Individual Number: Player may bet on any specific number from 1 to 6. If chosen number appears 1 time bet pays 1 to 1, if it appears 2 times bet pays 2 to 1, and if it appears 3 times it pays 3 to 1.

The critical step in calculating the odds in Sic Bo is to find the probability of any given total in the throw of three dice. Following is a formula for s spots over n dice, taken from The Theory of Gambling and Statistical Logic by Richard A. Epstein, formula 5-14.

For example, let's look at the number of ways to get 11 spots over 3 dice.

int[(s-n)/6] = int[(11-3)/6] = int[1.33] = 1

The total would be 6^-3 * [-1⁰*combin(3,0)*combin(11-6*0-1,3-1) + -1¹*combin(3,1)*combin(11-6*1-1,3-1) ] =
1/218 * [1*1*combin(10,2) + -1*3*combin(4,2)] =
1/218 * [1*1*45 + -1*3*6] =
1/218 * [45-18] = 27/216 = 12.50%

Sic Bo Results 2020

Alternatively, if you can program a computer that would probably be the fastest way to get the results.

Here is a simple function in C++.

Following is the output of the function.

If you don’t know how to program you’re going to have to do this the hard way. What I recommend is list every combination of 3 dice. To avoid the list being 6³=216 items long do not repeat the same combinations in different orders. In the interests of not listing the same number twice always order each combination from lowest to highest, not forgetting combinations with a pair or three of a kind.

So we start with 1,1,1.

Next would be 1,1,2.

Then 1,1,3; 1,1,4; 1,1,5; and 1,1,6.

Obviously you can’t roll a 7 with one dice so next we increment the second die.

1,2,?

The third die must be greater or equal to the second die so the next combination in full would be 1,2,2.

Next comes 1,2,3; 1,2,4; 1,2,5; and 1,2,6.

Then comes 1,3,3.

I hope you see the pattern. The whole list would look like the following.

Next we have to determine the number of permutations of each combination. A combination is a set without regard to order and a permutation is a set with regard to order.

With a three of a kind there is only one way permutation. For example if the three dice are 1,1,1 there is only one way to roll that a 1 each time.

If the combination is 1,1,2 there are three ways to roll that: 1,1,2; 1,2,1; and 2,1,1.

If all three dice are 1,2,3 there are six possible permutations: 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,1,2; 3,2,1

The general formula is that if you have a total of d dice and the totals of each number are x₁, x₂, x₃…x_n then the number of permutations are d!/(x₁!*x₂!*x₃*…*x_n). So the number of ways to get a three of a kind would be 3!/3! = 6/6 = 1. The number of ways to get a pair would be 3!/(2!*1!) = 6/(2*1) = 3. The number of ways to get three different numbers would be 3!/(1!*1!*1!) = 6/(1*1*1) = 6.

Next we go through the tedious process of adding the number of permutations for each total. For example a total of 6 has the following combinations with the corresponding number of permutations.

The final table will look like this, not unlike the result of the computer function earlier.

So now lets add a column to our list for the number of combinations of each set. Let’s also add a total for the three dice.

Now we can divide each total number permutations by the total number 3-dice permutations (216) to get the probability of each total.

Finally, we are ready to evaluate the expected value of each bet. The expected value is the ratio of the amount the player can expect to win to the amount he bets on any given bet. So a fair bet would an expected value of zero. A positive expected value would mean the player has the advantage. A negative expected value would mean the dealer has the advantage.

Let’s start with the 4 bet. This wins with a total of 4 and pays 60 to 1. For those who don’t know, '60 to 1' means if the player wins he wins 60 times his bet and KEEPS his original wager. Had the odds paid '60 for 1' the player would NOT keep his original bet. Most table games pay on a 'to 1' basis.

The probability of a total of 4 is 3/216 = 0.013889. Thus the probability of losing is 1-(3/216) = 1-0.013889 = 0.986111.

The expected value of any bet with only two possibilities, winning or losing, is:

(Probability of winning)*(Amount of win) + (Probability of losing)*(Amount of loss).

For the 4 bet the expected value is

0.013889 * 60 - 0.986111*-1 = -0.15278.

So, this tells us that for every dollar the player bets on a total of 4 he can expect to lose 15.278 cents on average. Or, the house edge is 15.278%.

The next table shows the expected value and how it was calculated for all bets of a total of 4 to 17.

Two of a kind

There are combin(6,2)=6!/(4!*2!)=15 ways to choose two numbers out of six. Each of these combinations is listed on the table and the player bet on as many as he wishes. If both numbers appear on the roll of the three dice then the player wins and is paid 15 to 1.

Let’s assume the player picks a 1 and 2 as his two numbers. What is the probability that both a 1 and 2 occur in the roll of 3 dice? One way to do this would be to note all the possible winning permutations:

Thus there are a total of 30 winning permutations.

There are 6³=216 total permutations, so the probability of winning is 30/216 = 1/36 = 0.1388889

The two of a kind bet pays 5 to 1. So the expected value is 0.1388889*5 + (1-0.1388889)*-1 = -0.16667. In other words the house edge is 16.67%.

Double

There are six double bets available, one for each number from 1 to 6. The player may be on any one or combination of bets. Any given bet wins if at least two of the three dice land on that number.

Let’s assume the player bets on the 1.

One way to solve it would be to note all the winning permutations:

Thus there are a total of 16 winning permutations.

There are 6³=216 total permutations, so the probability of winning is 16/216 = 0.0740741.

The double bet pays 10 to 1. So the expected value is 0.0740741*10 + (1-0.0740741)*-1 = -0.18518. In other words the house edge is 18.52% (ouch!).

Triple

Player may bet on any specific number (for example a 1). Player wins if all 3 dice land on that number.

There is obviously only one way to win this bet, so the probability of winning is 1/216 = 0.0046296. The bet pays 180 to 1 so the expected value is 0.0046296*180 + (1-0.0046296)*-1 = -0.16204. So the house edge is 16.204%.

Any Triple

The Any Triple bet pays if any three of a kind is thrown. There are obviously six winning combinations (1,1,1; 2,2,2; 3,3,3; etc.). So the probability of winning is 6/216 = 0.027778. The bet pays 30 to 1 so the expected value is 0.027778*30 + (1-0.027778)*-1 = -0.13889. So the house edge is 13.89%.

Low

The low bet wins if the total of the three dice is 3 to 10, without being a three of a kind. The probability of any total 10 or less is exactly 50%. The average number on any one die is (1+2+3+4+5+6)/6 = 21/6 = 3.5. So the average of three dice is 3*3.5 = 10.5. It stands to reason that the probability of getting under or over 10.5 is 50%.

However the bet loses on a three of a kind. There are 3 three of a kinds that would turn a winner into a loser: 1,1,1; 2,2,2; and 3,3,3. So the probability of having a total of 10 or less as a three of a kind is 3/216 = 0.0188889. So the overall probability of winning is 0.5 – 0.188889 = 0.4861111. The bet pays 1 to 1 so the expected value is 0.4861111*1 + (1-0.4861111)*-1 = -0.02778. Thus the house edge is 2.78%.

High

The high is just the opposite of the low bet, so it stands to reason the house edge would also be 2.78%.

Individual Number

Player may bet on any specific number from 1 to 6. If chosen number appears 1 time bet pays 1 to 1, if it appears 2 times bet pays 2 to 1, and if it appears 3 times it pays 3 to 1. Probability of 1 match is 34.72%, 2 matches is 6.94%, 3 matches is 0.46%.

Let’s assume the player picks the number one.

There is only one way to get three ones: 1,1,1. So the probability of three ones is 1/6³ = 1/216.

Following are the ways to get two 1’s and the number of permutations of each.

So the probability of two ones is 15/6³ = 15/216.

Following are the ways to get one 1 and the number of permutations of each.

So the probability of two ones is 75/6³ = 75/216.

Another way to arrive at the probability of one 1 would be find the probability that the first die is a one and the second and third are not:

Pr(one)*Pr(not one)*Pr(not one) = (1/6)*(5/6)*(5/6) = 25/216.

However the one could appear in the first, second, or third position, so multiply by 3: 3*(25/216) = 75/216.

The probability of rolling zero ones is Pr(not one)*Pr(not one)*Pr(not one) = (5/6)*(5/6)*(5/6) = (5/6)³ = 125/216.

The following return table shows the possible outcomes, and the number of combinations, probability, and return of each. The return is the product of the probability and the win or loss to the player.

So the total expected return is -0.0787, or the house edge is 7.87%.

Sic Bo section at the Wizard of Odds.
How to calcualte the 3-dice permutation in Visual Basic.

The ancient game of Sic Bo with multipliers up to x1000!

£998 Match Bonus

+111 Free Spins

• 2018 New Best Casino Award
• Bonus on first 2 deposits
• All EG games available
• Popular for Live Casino

18+ BeGambleAware, Gamble Responsibly

10% CASHBACK ALWAYS!

No String Attached!

• VIP Casino
• No Wagering Requirement
• 10% Cashback Daily
• Live Casino on Mobile

18+ BeGambleAware, Gamble Responsibly

£100 WELCOME BONUS

+10% Cashback

• New Casino in UK
• Perfect for mobile
• Classic Slots
• Double the fun

18+ BeGambleAware, Gamble Responsibly

100% UP TO £100

+10% Cashback

• British Live Dealers
• Lightning Roulette
• Great Customer Support
• Perfect For British Players

18+ BeGambleAware, Gamble Responsibly

Live Super Sic Bo is the first dice game by Evolution Gaming, the most successful live gaming provider worldwide. The live presenter game is based on the asian ancient game of Sic Bo. In a custom built studio three dice are shaken, while you bet on the possible outcome. How is this release by Evolution Gaming different form the regular Sic Bo? Here the multipliers make the whole difference. Rules might be similar to the regular game, but you need to adjust your strategy so you can get a multiplier up to x1000! At Super Sic Bo every game can be a big win.

Live Super Sic Bo Review

Evolution Gaming Super Sic Bo is a rather simple game, you can learn how it works in just a few rounds. However, it is highly entertaining, since the simplicity of the game is balanced on a rather complex betting grid. The many possible outcomes of the game make intelligent and strategic betting absolute priorities. You will have lots of fun trying to figure out patterns and trends and bet accordingly.

The game unfolds in a fantastic custom built studio, based on the colours of red and gold. The presenter does not interact with the dices, that are rolled in a completely automated way. There is no possible interference with the results of the game.

Live Super Sic Bo follows the rules of the classic game, but like in Lightning Roulette and Lightning Dice, there are random multipliers that spice up the game. When all bets are closed, random multipliers up to x1000 are applied to some of the numbers on the betting grid. Good luck!

It is true that multipliers are randomly applied to any possible bet, however x1000 multiplier is given only to a certain type of bet. We are talking about triple bets, the only betting strategy that will get you one of those x1000 multipliers. Different bets are allotted different multipliers - keep reading to find out all about it.

Best Casinos to Play Live Super Sic Bo

Sic Bo Results Ufc

Are you looking for the best casinos to play Super Sic Bo with bonus? Choosing the best casino for playing live is extremely important. Only the perfect casino can guarantee the quality you need for enjoying Super Sic Bo 100%. We are talking about safety, graphics and customer service. But also about having a fantastic experience from all devices, including your smartphone.

The online casinos for playing Super Sic Bo by Evolution gaming you find on our pages have all you need for relaxing and having a great time. They all hold a licence from the UKGC (UK Gambling Commission, the authority that regulates online gambling) and are 100% safe and reliable. They offer you the best possible gaming experience and great welcome bonuses for playing Super Sic Bo!

Interface and Betting Grid

Evolution Gaming is known as the best live casino provider around the world. One of the reasons for that is the quality of their streamed games, another is their interface, so easy to use and understand.

At the bottom of the screen is the Live Super Sic Bo interface. As per other Evolution Gaming titles, the interface is divided in three blocks. In the left side is the logo and the are where you can type what you want to say to the presenter. they will reply to you in real time, and that’s what makes the game so entertaining!

On the right hand side are the latest statistics. Here you can see the latest numbers that have come out, and get an idea of the latest results in the game. At the top of the columns is the total, while the three numbers underneath show the three numbers that have actually come out. You can also switch to a roadmap that shows you the trend f big and small bets. You can make this part of the interface bigger or smaller, according to the number of statistics you’d like to see.

Sic Bo Results Football

At the center bottom of the screen is the betting grid and the possible chips you can place on the grid. There is also a Repeat Button, that you can use if you have a set strategy and you just want to repeat it over several games, without placing your bets each time.

In Super Sic Bo, as in other live games by Evolution Gaming like Lightning Roulette and Lightning Dice, there is a very short time for betting, you have to pay attention not to loose any rounds! At the beginning of each game, the top od the interface will turn green. This is the time when you can place your bets. the game is fast paced and soon enough the bets will be closed. The interface will turn red and the game will start.

Betting in Super Sic Bo

If you’ve never played Sic Bo before, the betting grid might seem a bit difficult to understand. On top of it, in Live Super Sic Bo there are some special bets which are given a random multiplier up to x1000. Let’s have a look at the betting greed and possible bets, so you can choose which strategy suits you better.

Being the game really simple, is nice to have a challenging aspect to it: betting. The betting grid is quite complex, because you can bet on any possible outcome of the three dices. therefore there are many possible strategies you can apply to this game, finding the one that is a winner is the real challenge of the game!

Let’s see the possible bets:

• SMALL/BIG: here you can place a bet on the total result of the three dices. Small for a result of 4-10, or big for an outcome of 11-17.
• ODD/EVEN: this is one of the safest bets in he game. You place your bet on the outcome of the total of the three dices, odd or even.
• TRIPLE: here you bet the outcome of the game will be three dices with the same result. This is a hot bet, because only triples get multipliers up to x1000.
• TOTALS: here you bet on the precise outcome of the three dices added together. They are paid differently, according to the odds stated on the grid.
• DOUBLE: marked in the line “Two Dice 5:1”. Here you bet on the possible outcome of two out of the three dices. There a re many different possibilities, this is one of the bets that are more challenging and fun.
• SINGLE: at the bottom of the grid is the single bets. Here you bet on the outcome of one of the three dices. Is one of the simplest bets, that allows for betting on your favourite number or trending number.

Multipliers up to x1000

One of the main differences between Evolution Gaming’ Super Sic Bo and a regular Sic Bo game lies in the possibility of getting a random multiplier. This game, like many other successful titles by EG allows players to get multipliers up to x1000! This means that with a bit of luck and a good betting strategy you can get some serious wins here.

Sic Bo Results 2019

After having a close look to the betting grid, you’ll notice the multipliers only apply to certain numbers. An important thing to keep in mind is that you can get the x1000 multiplier only if you bet on a triple. There are no other bets that will give you such a big result. Another detail to keep in mind is that Random Multipliers do not apply to the Even bets.

Random Multipliers are not visible while you’re betting. They appear after all bets are closed, in the fashion of Lightning Roulette or Lightning Dice. They are completely unpredictable (ok, they follow some rules as we mentioned above) and they can get up to x1000. You need a lot of luck and good strategy for getting one of these multipliers, but the challenge of this game is right here!

Strategies for betting in Super Sic Bo

Live Super Sic Bo is a rather straightforward game. There is nothing difficult to understand in the unfolding on the game, which consists only in waiting for the dice shaker to stop and reveal the result of the round.

Super Sic Bo Results

While this is highly entertaining, the real challenge comes whit your betting strategy. There are so many possible outcomes, and so many possible betting numbers, you’ll have to take a decision and gamble strategically.

Let’s have a look at a few simple betting strategies. You will be able to use them or come up with a combination of more of those. Remember to select a bet size that can allow you to play for a long time, as the results of the game might not be as easily achieved as you think.

• PLAY SAFE: if you want to play for a long time and avid losing money, betting on even/odd or small/big can be a good strategy. This way you can keep playing for a long time without incurring in looses. You will not win big wither, but you’ll have the chance of enjoying yourself.
• CHASING THE X1000 MULTIPLIER: another possible strategy is betting on all triples and wait for the big multipliers. This is a highly risky strategy, you might be loosing some money before you get to win anything. However, you place yourself in the position of winning big and get your losses back with a high interest!
• MIXED STRATEGY: with this strategy you mix risky and safe bets. This way you can cash in on high risk bets, but also play safe and not give away too much of your bankroll with a safer bet. This seems to be the strategy that pays out the most on the long run.

Evolution Gaming Super Sic Bo RTP, Return to Player

It is always interesting to know what the return to player of a game is. This number, based on statistics for thousands of games, states the odds for a player to win a game.

In the case of Super Sic Bo by Evolution Gaming, the base game has a RTP of 97.22%. This is a high RTP compared to industry standard, meaning the game (calculated on the simple bets odd/even and big/small) has a quite favourable percentage of wins for players.